Les images optiques de Sentinel-2, avec leur revisite tous les cinq jours, leur résolution de 10 mètres, et leurs nombreuses bandes spectrales optiques, permettent d'estimer les caractéristiques du couvert végétal (surface foliaire verte par mètre carré (LAI), contenu en chlorophylle, orientation des feuilles...), et de suivre leurs variations. Pour extraire cette information, nous utilisons de plus en plus souvent des réseaux de neurones, qui apprennent à déterminer ces caractéristiques à partir d'exemples de référence. Cet article présente les méthodes classiquement utilisées pour cette application, puis une nouvelle méthode proposée par Yoël Zérah au cours de sa thèse au CESBIO encadrée par Jordi Inglada (CNES) et Silvia Valero (IRD).

Regression à partir de données in-situ

Dans les débuts de l'apprentissage automatique, les premiers résultats ont été obtenus en utilisant des informations collectées sur le terrain en même temps (ou presque) que l'observation du satellite. Mais collecter ces informations demande du temps et coûte cher. Les réseaux de neurones ont beaucoup de paramètres et les réseaux de neurones profonds en ont encore plus. Pour que l'apprentissage soit robuste, il faut plus d'une observation par paramètre à déterminer. L'utilisation de données de terrain oblige donc à limiter fortement la complexité du modèle, qui fournit donc un résultat souvent peu précis si le phénomène à modéliser est complexe.

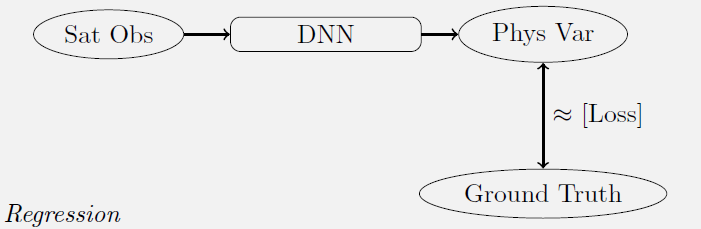
Données de référence générées par modèles physiques

Depuis quelques dizaines d'années, des méthodes de génération de données de référence par modèles ont vu le jour. Au lieu de collecter les données sur le terrain, on utilise un modèle physique (parfois approché) qui génère ces données. Par exemple le modèle PROSAIL, qui modélise la végétation comme un gaz de feuilles. Ce modèle est rapide, et le coût de génération des données d'apprentissage devient faible.

Cette méthode nécessite cependant beaucoup de travail : pour simplifier le réseau de neurones et éviter les risques d'erreur, il faut qu'il apprenne sur des données réalistes. Il est inutile de lui apprendre des cas qui ne se produisent jamais. Cependant, il faut beaucoup de détails pour distinguer des cas différents, mais ressemblants. Pour préparer les jeux de données d'apprentissage, il faut chercher les gammes de variation et de covariance des différents paramètres du modèle. Notre collègue Marie Weiss (INRAE) y a dédié plusieurs années de travaux, pour mettre au point le modèle BV-NNET, utilisé dans le logiciel SNAP de l'ESA, ou dans les produits de variables biophysiques qui seront bientôt distribués par THEIA.

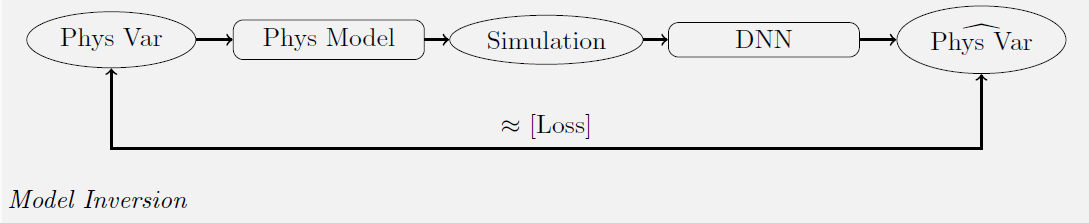
Une nouvelle méthode d'inversion du modèle SAIL

Yoel Zérah, lors de sa thèse au CESBIO encadrée par Jordi Inglada (CNES) et Silvia Valero (IRD), a mis au point une nouvelle méthode d'inversion du modèle PROSAIL. Elle consiste en fait à échanger les deux boîtes du diagramme précédent : modèle de régression et modèle physique (en réalité, c'est un peu plus compliqué que ça). Un réseau de neurones utilise les données Sentinel-2 pour déterminer des variables intermédiaires qui sont utilisées en entrée du modèle PROSAIL. Les paramètres du réseau sont optimisés pour minimiser les différences entre les données S2 en entrée et celles simulées par PROSAIL. Les variables intermédiaires obtenues en sortie du réseau de neurones sont donc les caractéristiques de la végétation recherchées, et les données utilisées dans l'apprentissage sont réalistes par nature puisqu'il s'agit de données réelles. Cette méthode économise donc la phase de mise au point du jeu d'apprentissage. La méthode est décrite avec davantage de détails dans cet article sur le blog du CESBIO.

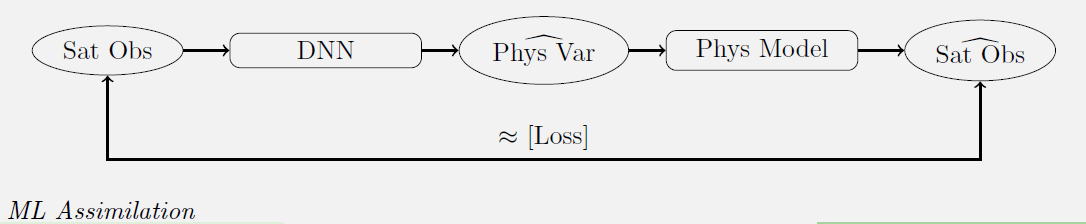
Validation des résultats

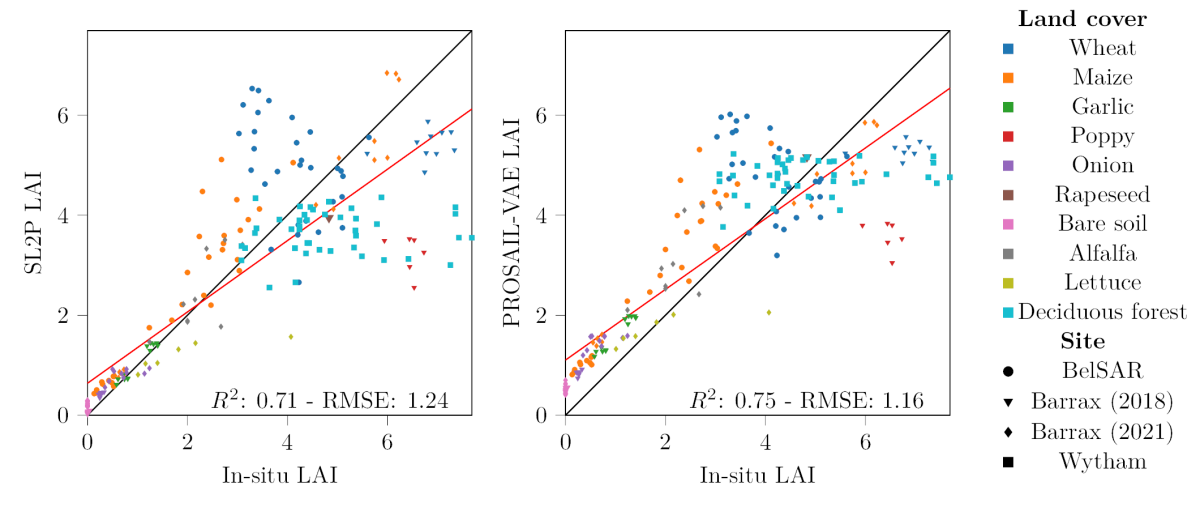
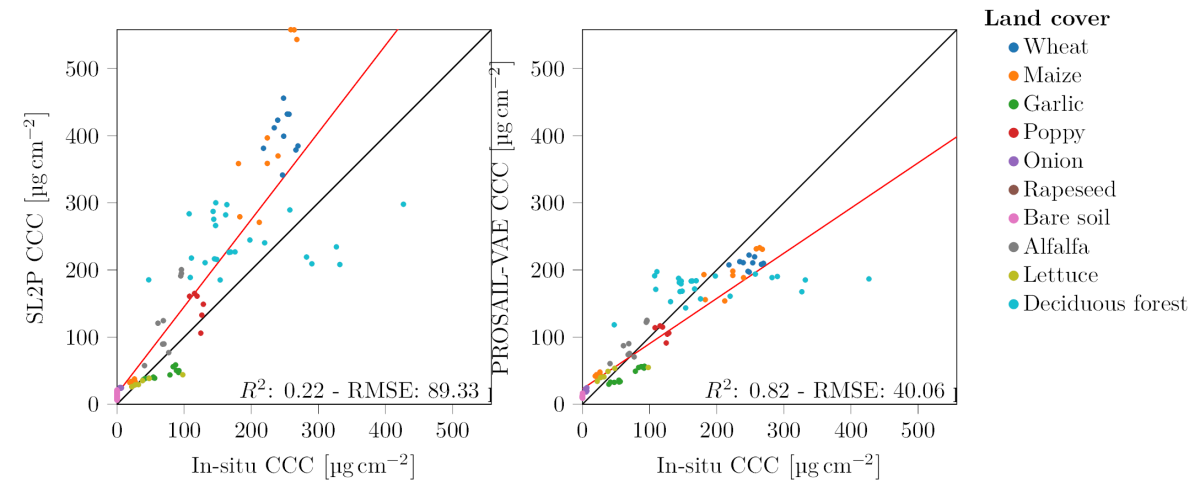
Les courbes ci-dessous montrent les résultats obtenus sur un grand nombre de données in-situ acquises sur différentes cultures. Sur l'indice de surface foliaire, les résultats ont des performances équivalentes à celle du modèle BV-NNET (avec un petit biais sur les sols nus pour le nouveau modèle). Sur l'estimation de la chlorophylle, les résultats sont bien meilleurs que ceux de BV-NNET. Le réseau a l'avantage de fournir toutes les variables en entrée du modèle PROSAIL, mais, malheureusement, il existe peu de données in-situ pour valider leurs performances. Il fournit aussi une estimation de la précision des résultats et peut permettre de générer les histogrammes des covariances entre variables de ce modèle.

Conclusion

En conclusion, ce travail a permis en moins d'un an d'obtenir des résultats très proches de l'état de l'art pour l'estimation du LAI, et même supérieurs pour le contenu en chlorophylle. Son énorme avantage est lié au fait que son apprentissage étant réalisé par de véritables observations, les distributions des variables sont réalistes par construction. Cette méthode nécessite toutefois que le modèle physique utilisé soit dérivable pour permettre d'y calculer les gradients.

Cet article volontairement simplificateur a été écrit par Olivier Hagolle, à partir d'un article de Yoel Zerah sur le blog du CESBIO, et de schémas fournis par Jordi Inglada.